W jednym z ostatnich wpisów poruszyłem temat sterowanego napięciowo źródła prądowego. Artykuł ten spotkał się z Waszym dużym zainteresowaniem - i za to bardzo dziękuję! 😁 Wiele osób zadawało pytania, prosiło o doprecyzowanie niektórych kwestii oraz o dalsze kontynuowanie tematu.
Tym razem chciałbym skupić się na zredukowaniu błędu, wprowadzanego do układu przez zastosowane przeze mnie wzmacniacze operacyjne.
Jeśli temat jest Ci całkowicie nieznany, zacznij od lektury poniższych wpisów:
- Źródło prądowe w elektronice.
- Tranzystorowe źródło prądowe w praktyce.
- Źródło prądowe sterowane napięciowo.
Przypomnienie najważniejszych kwestii
Ostatnim razem przedstawiłem schemat elektryczny sterowanego źródła prądowego wraz z niezbędnymi obliczeniami oraz symulacjami. Przypomnę więc cztery najważniejsze rzeczy, które będą potrzebne do dalszej analizy, rozpoczynając od założeń :-)
Założenia:
- napięcie zasilające: 12 V,
- zakres prądów wyjściowych: 0 mA - 200 mA (tolerancja 1% ),
- rozdzielczość: 1 mA,
- zakres napięć sterujących: 0 V - 2.5 V,
- rezystancja obciążenia: 1 Ohm (docelowo zmienna w pewnym zakresie),
- rezystancja obciążenia podłączana jest do masy układu.
Na podstawie powyższych założeń powstał schemat:
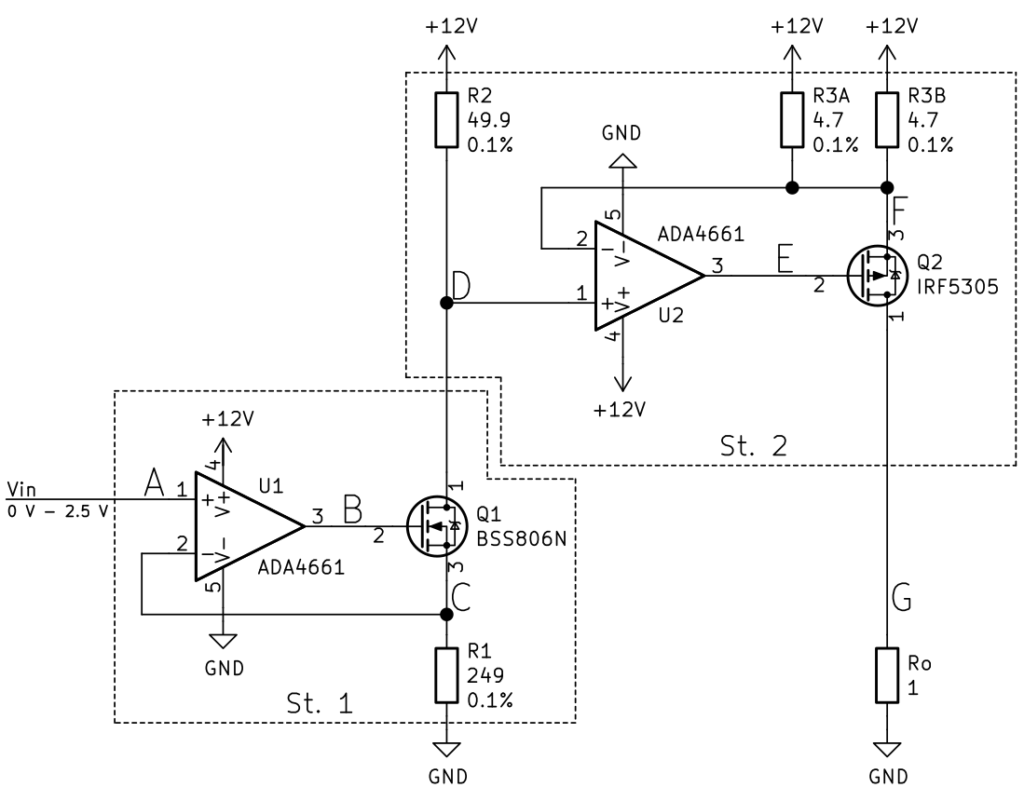
Prąd na wyjściu układu (czyli prąd płynący przez rezystor Ro) zależny jest od napięcia wejściowego i można go wyliczyć stosując poniższy wzór:
Posługując się wzorem (1) popełniamy błąd, którego wielkość jest zależna od napięcia wejściowego:
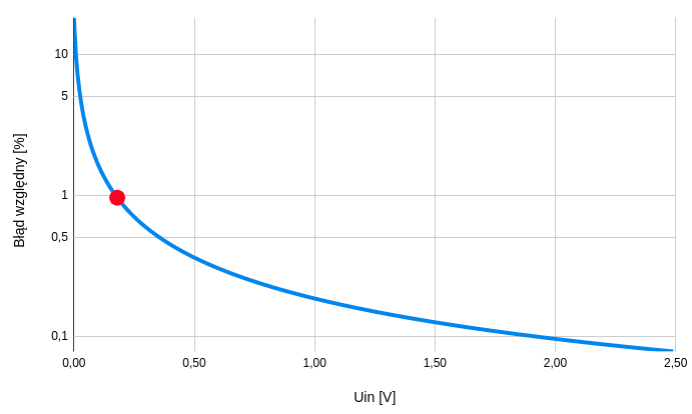
Powyższy wykres mówi o ile procent różni się wartość prądu na wyjściu układu od oczekiwanej, dla danej wartości napięcia na wejściu. Zgodnie z założeniami wartość tego błędu nie powinna przekraczać 1 %. Problemem jest zakres napięć mniejszych od 0.18 V - tutaj błąd osiąga wartości nawet kilkunastu procent. Jeśli jesteś zainteresowany dokładniejszymi rozważaniami na temat tego skąd bierze się błąd - zajrzyj tutaj.
Minimalizacja błędu
Pomysłów na zmniejszenie błędu poniżej oczekiwanej wartości (1 %) może być wiele.
Jednym z nich może być pomiar spadku napięcia na rezystorze R3 poprzez przetwornik analogowo-cyfrowy, implementację regulatora PI w mikrokontrolerze oraz odpowiednie wysterowanie wejścia układu, aby zmniejszyć uchyb do zera. Takie rozwiązanie z pewnością zadziała. Jest to jednak spora komplikacja programu sterującego - a to wydaje się być zbędne dla tak prostego układu.
Biorąc pod uwagę fakt, że wartość bezwzględna błędu jest w przybliżeniu stała dla całego zakresu napięć sterujących, zdecydowałem się rozwiązanie łatwiejsze - pomiar prądu płynącego przez rezystor wzorcowy (tolerancja 0.1 %), przed każdym załączeniem obwodu wyjściowego, przeliczenie jakiemu napięciu wejściowemu odpowiada różnica prądów oraz dodanie tej wartości do wejścia. Do wcześniej zaprezentowanego układu należy dodać układ pozwalający na załączanie i wyłączanie wyjścia oraz na załączanie i wyłączanie precyzyjnego rezystora pomiarowego. Pomiar napięcia na rezystorze wzorcowym będzie wykonywany dla prądu 10 mA. Przykład realizacji widoczny jest poniżej.
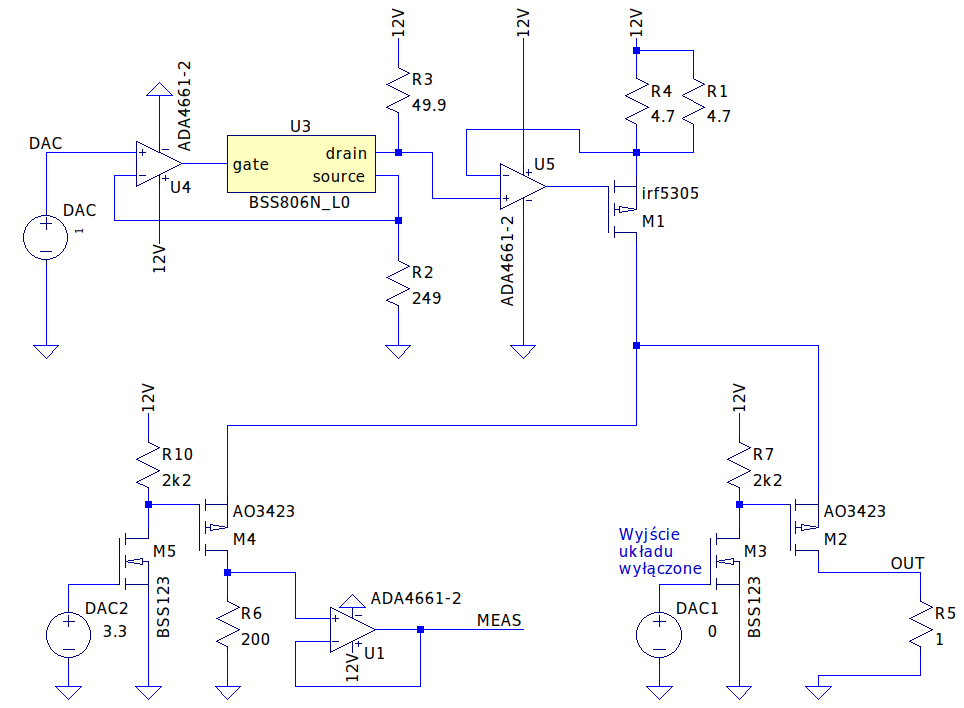
Wyjściem układu jest prąd płynący przez rezystor R5. Tym razem jednak wyjście te jest załączane poprzez dodatkowy tranzystor M2. Tranzystor M3 ma umożliwić sterowanie poprzez napięcia 0 V (wyłączony) oraz 3.3 V (załączone wyjście).
Bliźniaczy układ (M4, M5) został zastosowany do załączania precyzyjnego rezystora pomiarowego R6 (tolerancja 0.1%). Tutaj dodatkowo podłączony jest wzmacniacz operacyjny, który posłuży do pomiaru napięcia (poprzez ADC) na rezystorze R6. Wartość rezystora R6 została wybrana tak, aby przy prądzie testowym (10 mA), wystąpił na nim spadek napięcia ok. 2 V (w celu wykonania pomiaru poprzez ADC).
Jak wspomniałem wcześniej błąd bezwzględny jest stały dla całego zakresu napięć wejściowych - jak na rysunku poniżej.
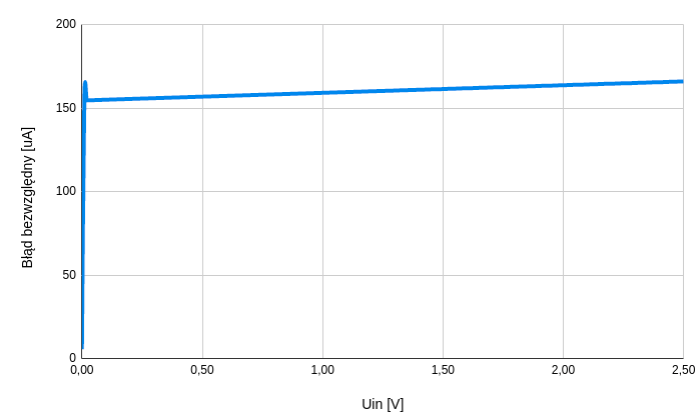
Wartość średnia tego błędu wynosi 160 uA - i nie jest powiedziane, że tak samo będzie w realnym układzie! Błąd zależy od napięcia offsetu wzmacniacza operacyjnego i może się zmieniać dla różnych egzemplarzy tego samego wzmacniacza. Zakładając, że błąd jest stały to, po zmierzeniu realnej wartości płynącego prądu, można go skompensować.
Wartość rezystora R6 została dobrana dla prądu o wartości 10 mA. Niezależnie od tego czy pożądanym prądem wyjściowym będzie 1 mA czy 200 mA, kompensacja będzie odbywała się z użyciem 10 mA.
Przykład obliczeń
Przy każdorazowym załączeniu źródła wystąpi następująca sekwencja zdarzeń.
1. Obliczenie napięcia wejściowego zgodnie ze wzorem (1)
2. Wyłączenie wyjścia układu.
Wyjście układu - czyli tranzystor M2 musi zostać wyłączone. Prąd płynący przez ten układ, gdy tranzystor jest wyłączony, jest rzędu pA - można go pominąć w obliczeniach.
3. Podłączenie wzorcowego rezystora do wyjścia układu.
Tranzystor M4 musi zostać załączony, aby umożliwić przepływ prądu przez rezystor R6.
4. Podłączenie do wejścia źródła wyliczonego napięcia: 117.3 mV.
5. Pomiar napięcia na rezystorze R6.
Docelowo pomiar napięcia będzie realizowany poprzez przetwornik analogowo-cyfrowy. W celach demonstracyjnych wystarczy symulacja. Poniżej widoczne jest zmierzone napięcie 1.969 V.
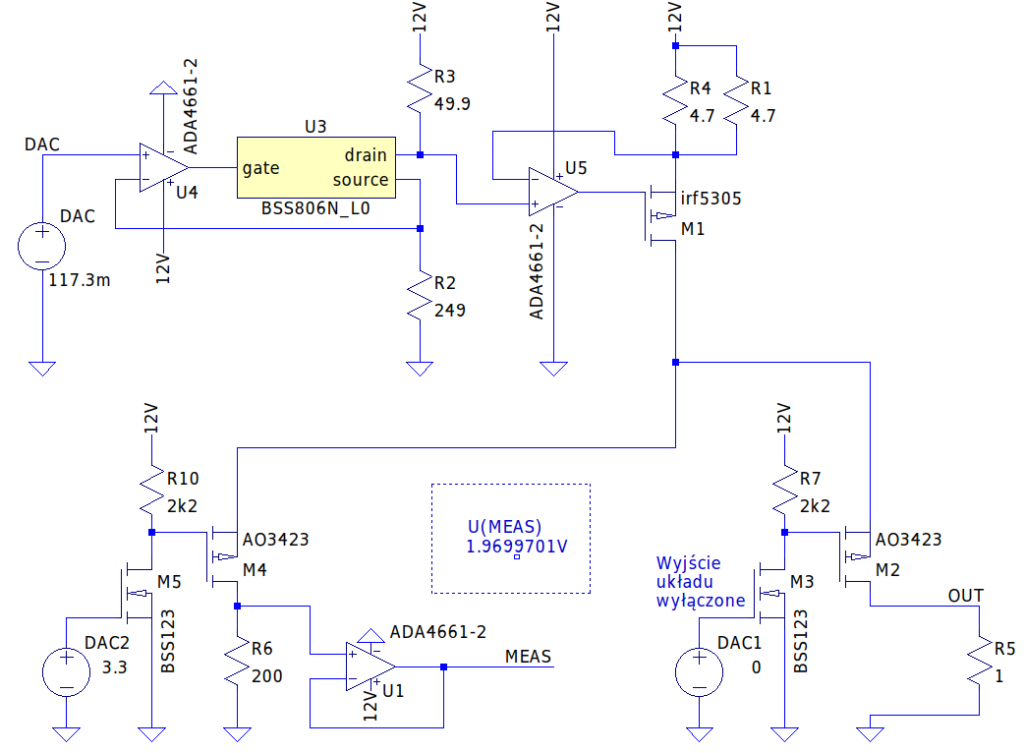
6. Obliczenie prądu płynącego przez R6.
Następnie można z prawa Ohma obliczyć jaki prąd płynie przez rezystor R6.
7. Obliczenie błędu bezwzględnego.
Wiedząc, że pożądaną wartością prądu jest 10 mA, możemy obliczyć wartość błędu bezwzględnego.
8. Obliczenie jakiej wartości napięcia wejściowego odpowiada błąd - zgodnie ze wzorem (1).
Powyżej obliczony został błąd. Wiadomo, że prąd na wyjściu jest niższy o 155 uA od oczekiwanego. Aby go skompensować należy zwiększyć napięcie wejściowe. Należy się dowiedzieć o ile trzeba zwiększyć napięcie na wejściu, aby zmniejszyć błąd. Do tego można posłużyć się wzorem (1).
9. Obliczenie wartości napięcia wejściowego z kompensacją.
W punkcie wyliczyliśmy wartość napięcia wejściowego. Teraz należy do niej dodać napięcie wyliczone w punkcie 8.
10. Odłączenie od układu rezystora wzorcowego.
Po obliczeniu poprawnej wartości napięcia, rezystor wzorcowy może zostać odłączony. Po wyłączeniu tranzystora M4 przez rezystor R6 będzie płynął prąd rzędu pA - nie będzie więc wpływał na poprawność funkcjonowania układu.
11. Podłączenie obciążenia układu.
Obciążenie układu może zostać teraz podłączone - czyli tranzystor M2 zostanie włączony. Do wejścia układu podłączone zostanie wyliczone w punkcie 9 napięcie: 119.1 mV.
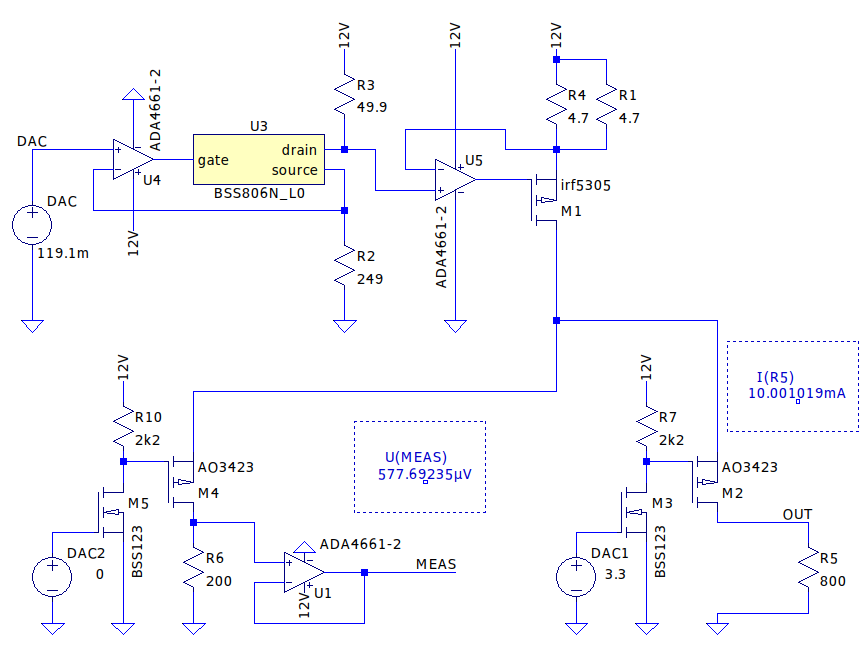
Na symulacji widoczna jest wartość prądu płynącego przez rezystor R5 (wyjście układu) po kompensacji. Teraz wynosi ona 10.001 mA - i to jest świetny wynik! Aktualny błąd względny wynosi praktycznie 0%! Dla porównania - wcześniej dla napięcia wejściowego 120 mV błąd był równy 1.5%. Różnica jest ogromna!
Może się wydawać, że do wykonania jest bardzo dużo operacji, ale dla układu z mikrokontrolerem nie jest to problemem - tym bardziej, że są to obliczenia jednorazowe, a nie ciągłe :-)
Podsumowanie
Przedstawione rozwiązanie na skompensowanie błędu spowodowanego przez napięcie offset'u wzmacniaczy operacyjnych nie należy do idealnych, ani odkrywczych :-) Jest jednak łatwe i szybkie w wykonaniu - a przede wszystkim skuteczne!
Masz może inny, ciekawszy pomysł na zminimalizowanie błędu? Podziel się nim! Chętnie się z nim zapoznam! :-)