Źródło prądowe sterowane napięciowo

Sterowane źródło prądowe może być bardzo przydatnym narzędziem laboratoryjnym w pracowni elektronika. Nie jest jednak tak popularne jak wszechobecne źródła napięcia. Dobrą wiadomością jest to, że na własne potrzeby, można je w łatwy sposób skonstruować.

W tym wpisie przedstawię przykład realizacji sterowanego napięciowo źródła prądowego wraz z podstawowymi obliczeniami. Podobnie jak w przypadku przedstawionych ostatnio tranzystorowych źródeł prądu, tutaj również przyjmę pewne założenia dla projektowanego układu.

Założenia:

napięcie zasilające: 12 V,
zakres prądów wyjściowych: 0 mA - 200 mA (tolerancja 1% ),
rozdzielczość: 1 mA,
zakres napięć sterujących: 0 V - 2.5 V,
rezystancja obciążenia: 1 Ohm (docelowo zmienna w pewnym zakresie),
rezystancja obciążenia podłączana jest do masy układu.

Jeśli temat źródeł prądowych jest Ci obcy, zachęcam do rozpoczęcia czytania od poniższych wpisów:

Spis treści

Sterowane źródło prądowe
Jak działa układ?
Obliczenia
Symulacje
Co jest powodem błędu? - pułapki
Podsumowanie

Sterowane źródło prądowe

Sterowane źródło prądowe można zrealizować na różne sposoby - tak jak każdy inny układ elektroniczny. Poniżej przedstawiony układ przetwarza wejściowe napięcie sterujące, w zakresie od 0 V do 2.5 V, na prąd płynący z wyjścia układu - w zakresie od 0 mA do 200 mA. Samo sterowanie (napięcie) może być zrealizowane poprzez potencjometr, sygnał PWM lub przetwornik cyfrowo-analogowy.

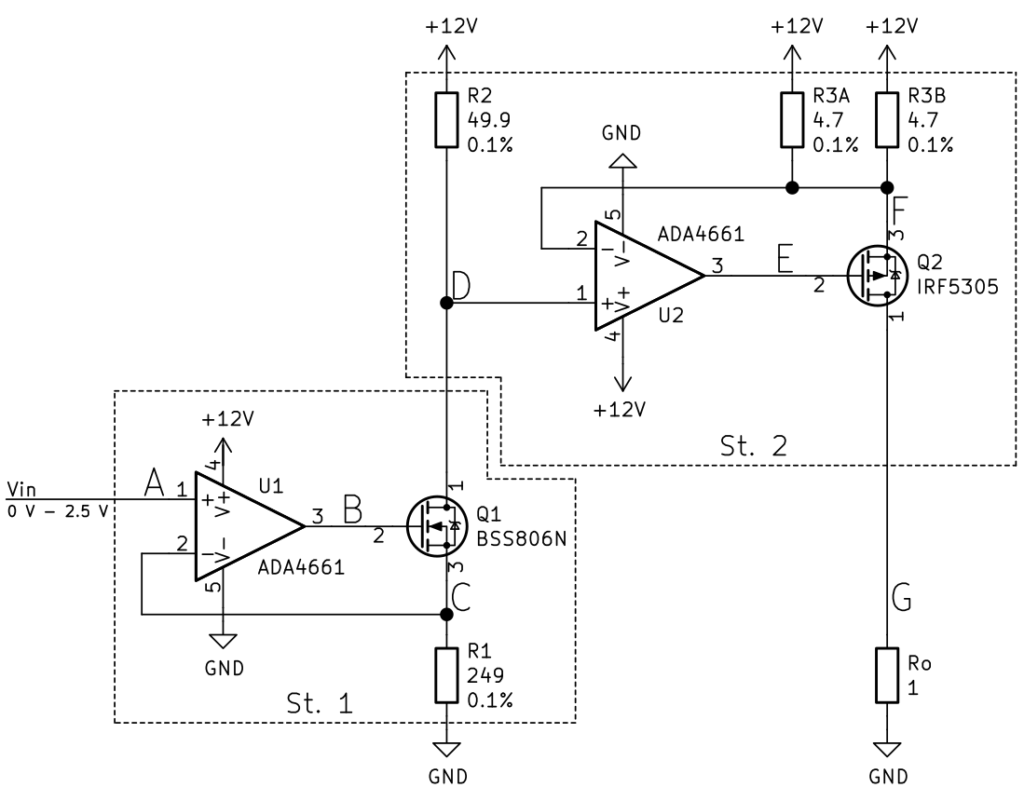
Jak działa układ?

Układ przedstawiony na rysunku 1 składa się z dwóch głównych bloków funkcjonalnych:

Blok konwertujący napięcie sterujące na prąd referencyjny (oznaczony jako St. 1).
Blok wzmacniający prąd referencyjny (oznaczony jako St. 2).

Blok 1 - wytwarzanie prądu referencyjnego

Pierwszy blok układu składa się ze wzmacniacza operacyjnego (U1), tranzystora MOSFET (Q1) z kanałem N oraz rezystora (R1). Jego zadaniem jest wytworzenie prądu referencyjnego, który w kolejnym bloku zostaje odpowiednio wzmocniony.

Doprowadzając napięcie do wejścia układu (punkt A na schemacie) powstaje różnica potencjałów na wejściach wzmacniacza operacyjnego U1. Wejście odwracające podłączone jest pomiędzy tranzystor Q1 i rezystor R1 (punkt C). Wzmacniacz "za wszelką cenę dąży" do tego, aby napięcia na jego wejściach były równe (czyli napięcia w punktach A i C). Na przedstawionym schemacie, wzmacniacz będzie chciał wytworzyć na rezystorze R1 spadek napięcia równy napięciu na jego wejściu nieodwracającym. W związku z tym, zacznie zwiększać napięcie na swoim wyjściu (punkt B), jednocześnie sterując bramką tranzystora Q1. Przy odpowiednim poziomie napięcia na bramce tranzystora, zaczyna on przewodzić prąd. To z kolei spowoduje przepływ prądu przez rezystor R1, a co za tym idzie - pojawienie się spadku napięcia. Wzmacniacz będzie zwiększał napięcie na swoim wyjściu do czasu aż spadek napięcia na rezystorze R1 będzie równy napięciu wejściowemu.

U_{IN} = U_{R1}

(1)

Ponieważ zastosowana została pętla ujemnego sprzężenia zwrotnego, obliczenia płynącego przez rezystor R1 prądu, będącego prądem referencyjnym w układzie, sprowadzają się do jednego działania.

I_{REF} =I_{R1} = \frac{U_{IN}}{R_1}

(2)

Jest to prąd referencyjny, który nie płynie przez obciążenie. Aby ograniczać straty, jego wartość powinna być możliwie mała (a na pewno dużo mniejsza od prądu wyjściowego).

Blok 2 - wzmacnianie prądu

Drugi blok układu składa się ze wzmacniacza operacyjnego (U2), tranzystora MOSFET (Q2) z kanałem P oraz rezystorów (R2, R3). Jego zadaniem jest wzmocnienie prądu referencyjnego, i przekazanie go do wyjścia układu. Pełni funkcję precyzyjnego wzmacniacza prądowego, w którym wzmocnienie ustalają rezystory R2 i R3.

Wytworzony prąd referencyjny, płynący przez rezystor R1, płynie również przez rezystor R2, powodując powstanie na nim spadku napięcia.

U_{R2} = I_{REF}*R_2

(3)

Napięcie z punktu D, będące różnicą pomiędzy napięciem zasilania i spadku napięcia na rezystorze R2, jest podłączone do wejścia nieodwracającego wzmacniacza U2.

U_D = U_Z-U_{R2}

(4)

Powoduje to powstanie różnicy potencjałów na wejściach wzmacniacza. Wzmacniacz ten, podobnie jak w bloku 1, dąży do wyrównania tych napięć - steruje więc swoim napięciem wyjściowym (punkt E) tak, żeby przez tranzystor Q2 oraz rezystor R3 (na schemacie widnieje równoległe połączenie dwóch rezystorów) popłynął taki prąd, aby napięcia w punktach D oraz F były równe. Alternatywnie można powiedzieć, że wzmacniacz dąży do wyrównania spadków napięć na rezystorach R2 oraz R3.

U_{R2} = U_{R3}

(5)

Znając wartość spadku napięcia na rezystorze R3, oraz samą wartość rezystancji R3, można wyliczyć wartość prądu wyjściowego.

I_{OUT} = \frac{U_{R3}}{R_3}

(6)

Łącząc ze sobą wzory (3), (5) i (6) można napisać:

I_{OUT} = I_{REF}*\frac{ R_2}{R_3} = I_{REF} * K

(7)

gdzie K jest wzmocnieniem prądowym układu.

K= \frac{ R_2}{R_3}

(8)

Na koniec wystarczy znaleźć zależność między prądem wyjściowym a napięciem wejściowym. Można to zrobić łącząc ze sobą wzory (2) oraz (7).

I_{OUT} = \frac{U_{IN}}{R_1}*\frac{ R_2}{R_3}

(9)

Obliczenia

Obliczenia należy wykonać dla maksymalnej wartości prądu wyjściowego: 200 mA. Taka wartość prądu ma być osiągalna przy maksymalnej wartości napięcia wejściowego: 2.5 V. Takie są założenia. W praktyce jednak posługujemy się znormalizowanymi wartościami rezystancji, a to będzie skutkowało niewielką rozbieżnością. Warto obliczyć układ tak, żeby dla maksymalnej wartości napięcia na wejściu, prąd wyjściowy był wyższy od oczekiwanego. Pozwoli to na ewentualne korekty/kalibracje programowe - jeśli sterowanie będzie oparte o mikrokontroler.

Zakładam, że maksymalny prąd referencyjny ma wynosić 10 mA. Będzie się on zmieniał wraz ze zmianą napięcia wejściowego - od 0 m A do 10 mA.

I_{REF_{MAX}} = 10 mA

(10)

Znając wartość prądu referencyjnego oraz spadku napięcia na rezystorze R1 (bo jest on równy napięciu wejściowemu - patrz wzór (1)), możemy wyznaczyć wartość rezystora R1 (prawo Ohma).

R_{1} = \frac{U_{IN_{MAX}}}{I_{REF_{MAX}}}=\frac{2.5}{0.01}

(11)

R_1 =250 \approx 249 \Omega

(12)

Patrząc na znormalizowane szeregi wartości, najbliższą 250 Ohmów jest wartość 249 Ohmów. Taka wartość zostaje więc wybrana. Ma to nieznaczny wpływ na zmianę prądu referencyjnego, który w rzeczywistości wyniesie:

I_{REF_{MAX}} = \frac{2.5}{249}\approx10.04 mA

(13)

W następnym kroku musimy założyć maksymalną wartość spadków napięć na rezystorach R2 i R3 (przypominam, że wartości te będą takie same - patrz wzór (5)). Wartość ta nie może być ani zbyt mała, ani zbyt duża. Jaką więc wybrać? Pamiętaj, że im większy spadek napięcia na rezystorze R3, tym mniejsza będzie maksymalna wartość rezystancji obciążenia jaką źródło będzie w stanie "obsłużyć". Zakładam więc, że maksymalna wartość spadku napięcia będzie wynosiła 0.5 V.

U_{R2_{MAX}} = U_{R3_{MAX}} = 0.5 V

(14)

Znając spadek napięcia na rezystorze R2 oraz wartość prądu referencyjnego, możemy obliczyć wartość rezystancji R2:

R_{2} = \frac{U_{R2_{MAX}}}{I_{REF_{MAX}}}=\frac{0.5}{0.01004}

(15)

R_2 \approx 49.8 \approx 49.9 \Omega

(16)

Wartość 49.9 Ohmów, wybrana została z szeregu E96. Następnie ze wzoru (7) musimy wyznaczyć niezbędne wzmocnienie prądowe układu.

K = \frac{I_{OUT_{MAX}} }{I_{REF_{MAX}}} = \frac{0.2}{0.01004}

(17)

K \approx 19.9 A/A

(18)

Ostatnią rzeczą do zrobienia jest wyznaczenie ze wzoru (8) wartości rezystancji R3:

R_3 = \frac{R_2}{K}=\frac{49.9}{19.9}\approx 2.507\Omega

(19)

Zgodnie z tym co wspomniałem wcześniej - "warto obliczyć układ tak, żeby dla maksymalnej wartości napięcia na wejściu, prąd wyjściowy był wyższy od oczekiwanego" - wartość obliczonej rezystancji R3 powinna być nieco niższa od wyliczonej. Ja wybrałem dwa równolegle połączone rezystory 4.7 Ohm, które dają łącznie 2.35 Ohm. Realne wzmocnienie układu wyniesie więc:

K = \frac{R_2}{R_3}=\frac{49.9}{2.35}\approx 21.23

(20)

Na koniec możemy skorzystać ze wzoru (9), aby widzieć zależność prądu wyjściowego od napięcia wejściowego.

I_{OUT} = U_{IN}*\frac{ R_2}{R_1*R_3}

(21)

I_{OUT} = U_{IN}*\frac{ 49.9}{249*2.35}

(22)

I_{OUT} = U_{IN}*0.08528

(23)

Jeśli napięcie wejściowe wyniesie 2.5 V (czyli nasza maksymalna wartość) to prąd na wyjściu powinien być równy:

I_{OUT} = 2.5*0.08528=213.2 mA

(24)

I to wszystko! :-) Regulując napięcie na wejściu od 0 V do 2.5 V, na wyjściu układu zmierzymy prądy w zakresie od 0 mA do 213.2 mA. I jest to zależność liniowa.

Symulacje

Żeby potwierdzić czy powyższe obliczania są słuszne - posłużę się symulacją! :-)

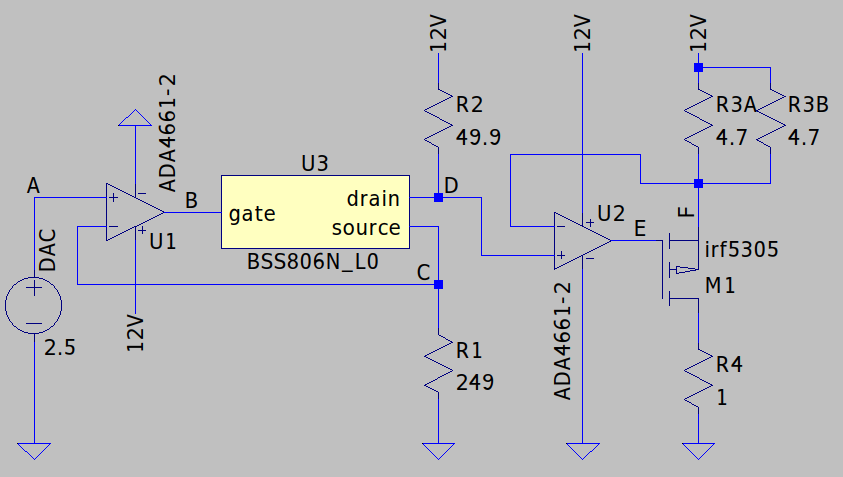
Rys. 2. Schemat zastosowany do symulacji układu.

Na podstawie przedstawionego powyżej układu wykonałem symulację DC Sweep, w której zmieniana jest wartość napięcia źródła oznaczonego jako DAC - czyli nasze napięcie wejściowe. Inaczej mówiąc sprawdzałem zależność:

I_{OUT} = f(U_{WE})

(25)

Mała uwaga - prąd wyjściowy to prąd płynący przez rezystor R4.

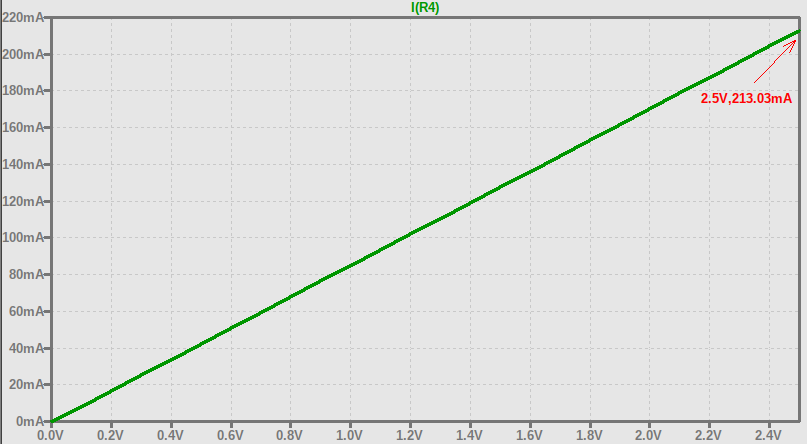
Rys. 3. Zależność prądu wyjściowego od napięcia wejściowego.

Symulacja potwierdza, że przedstawiona zależność jest liniowa. Dodatkowo dla napięcia wejściowego 2.5 V na wyjściu płynie prąd 213.03 mA - przedstawione obliczenia różnią się od symulacji o zaledwie 170 uA!

Czy jest to świetny wynik? To zależy...

Dlaczego twierdzę, że "to zależy"? Ponieważ porównując 170 uA do 200 mA, błąd ten jest praktycznie pomijalny i wynosi 0.085 %. Porównując 170 uA do 1 mA - błąd jest bardzo zauważalny. W tym przypadku wynosiłby aż 17 %.

Sprawdźmy zatem czy błąd bezwzględny (czyli różnica pomiędzy tym co chcemy uzyskać - wg obliczeń - a tym co zostało wyliczone przez symulator) jest stały dla całego zakresu napięć wejściowych.

Wspomnę jeszcze, że błąd ten wyliczam następująco (CALC - wartość obliczona, SYM - wartość z symulacji):

\Delta=|I_{OUT_{CALC}}-I_{OUT_{SYM}}|[A]

(26)

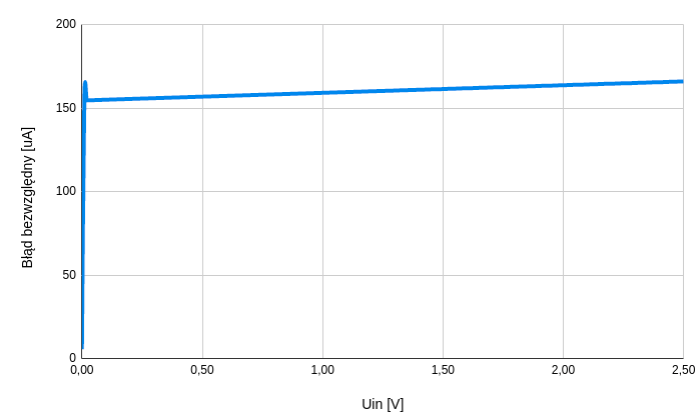
Rys. 4. Błąd bezwzględny - rozbieżność między obliczeniami, a symulacją.

Na wykresie widzimy, że praktycznie dla całego zakresu napięć wejściowych, błąd bezwzględny jest (w przybliżeniu) stały i wynosi około 160 uA. I nie jest to dobra wiadomość :-( Dlaczego? Spójrz na wykres błędu względnego, który pokazuje jak wygląda błąd w procentach. Do obliczeń zastosowałem wzór:

\delta=\frac{\Delta} {I_{OUT_{CALC}}}*100 \%

(27)

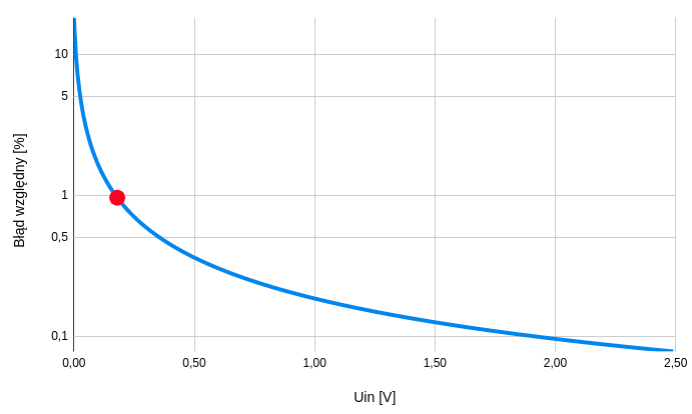
Rys. 5. Błąd względny - rozbieżność między obliczeniami, a symulacją - w procentach.

Jak widać, dla napięć wejściowych o wartościach poniżej 0.25 V, wartość prądu wygenerowanego na wyjściu układu, będzie znacznie odbiegała od obliczonych wartości i oczekiwań (1% tolerancji - zgodnie z założeniami). Zgodnie z wykresem na rysunku 5, błąd 1 % jest osiągany dla napięć wejściowych powyżej 0.18 V (czerwony punkt na wykresie). Czyli układ będzie działał prawidłowo w zakresie prądów wyjściowych od około 15 mA do 200 mA (sprawdź na rysunku 3).

Czy to kompletnie dyskwalifikuje układ? Oczywiście nie. Ponieważ wartość bezwzględna błędu jest w przybliżeniu stała (rys. 4), dla prądów mniejszych niż 15 mA, będzie można wprowadzić korektę programową (sterowanie przetwornikiem cyfrowo-analogowym, lub sygnałem PWM) i zmniejszyć ten błąd do akceptowalnego poziomu - mniejszego niż 1 %.

Co jest powodem błędu? - pułapki

Błąd bezwzględny generowania prądu na wyjściu wynosi 160 uA, w praktycznie całym zakresie napięć wejściowych. Z czego ten błąd wynika?

Napięcie offset'u

Głównym powodem błędu jest jeden z parametrów wzmacniacza operacyjnego - input offset voltage. Jego wartość jest zawsze podawana w dokumentacji technicznej. Obecność tego napięcia jest skutkiem niedopasowania wewnętrznych elementów wzmacniacza. Najprościej mówiąc, skutkuje to zwiększeniem się napięcia wyjściowego - o podaną wartość offsetu. Dla przykładu: jeśli napięcie offsetu wzmacniacza wynosi 1 mV, to napięcie te pojawi się na wyjściu - nawet jeśli wejście będzie podłączone do GND układu.

Dla wybranego przeze mnie wzmacniacza - ADA4661 - napięcie te wynosi (maksymalnie) 600 uV - taki jest najgorszy zmierzony przez producenta przypadek.

Patrząc na schemat układu, dla napięcia wejściowego 2.5 V, spadek napięcia na rezystorze R2 wyniesie 0.5 V (tak to obliczyliśmy wcześniej). Napięcie w punkcie D (rys. 1) jest więc równe 11.5 V. Wzmacniacz dąży do tego, żeby napięcie w punkcie F było identyczne. Tu powstaje problem. Napięcie offsetu (maksymalnie 600 uV) zostanie dodane do wyjścia wzmacniacza. To spowoduje, że napięcie w punkcie F, w rzeczywistości będzie wyższe - a więc spadek napięcia na rezystorze R3 będzie niższy. Jeśli spadek napięcia będzie niższy, to prąd płynący przez obwód również będzie niższy - i to jest przyczyna problemu.

Przeanalizuj to ze schematem. Zastanów się również jak duży wpływ na prąd wyjściowy miałoby użycie wzmacniacza z napięciem offsetu większym od 10 mV - nie jest to wysoka wartość.

Czy wybrany przeze mnie wzmacniacz jest idealny do tego rozwiązania? Powiedziałbym, że jest wystarczający. Na rynku dostępne są wzmacniacze z dożo mniejszym napięciem offsetu, lecz zazwyczaj idzie to w parze z ich wyższą ceną. W tym przypadku zakładam dokalibrowanie urządzenia programowo - co jest zadaniem stosunkowo łatwym i nie podnoszącym kosztów.

Jest jeszcze klika parametrów, na które powinieneś zwrócić uwagę.

Maksymalne napięcie wejściowe i wyjściowe wzmacniacza

Wzmacniacz operacyjny (szczególnie U2), w przedstawionym układzie, musi być w stanie wygenerować napięcia sięgające napięcia zasilającego. Takie samo zastrzeżenie ma miejsce w przypadku jego wejść. Do wejścia wzmacniacza U2 podłączane są napięcia 11.5 - 12 V. Zwróć więc uwagę na to, żeby wybrany przez Ciebie wzmacniacz był w stanie takie napięcia obsługiwać. Możesz wybrać wzmacniacze typu Rail-to-Rail, lub zastosować dla wzmacniacza osobne zasilanie, wyższe od napięcia na rezystorze R3.

Dla przykładu, wyobraź sobie, że wzmacniacz U2 może wygenerować na wyjściu maksymalne napięcie równe (Uz - 1.5 V) - tak to jest często podawane w dokumentacji. Jeśli zasilanie układu Uz wynosi 12 V, to na wyjściu pojawi się maksymalnie 10.5 V. Jaki będzie skutek? Napięcie pomiędzy bramką i źródłem tranzystora Q2 będzie wynosiło -1.5 V. Część tranzystorów przy takim napięciu może przewodzić prąd rzędu wielu amperów - wtedy nie będziesz miał kontroli nad prądem wyjściowym (nawet jeśli na wejściu układu będzie 0 V).

Nie bagatelizuj więc parametrów, które zazwyczaj znajdziesz w dokumentacji pod nazwami: Input Voltage Range oraz Output Voltage Range.

Tolerancja rezystorów

Wszystkie zastosowane w układzie rezystory mają realny wpływ na precyzję układu. Stosowanie rezystorów z tolerancją 10% z pewnością nie jest najlepszym rozwiązaniem. Użyj rezystorów 1% lub 0.1%.

Moc i temperatura

W zależności od podłączonego do układu obciążenia, na tranzystorze Q2, będzie wydzielała się moc - w postaci ciepła. Źródło prądowe, przedstawione w tym wpisie, z pewnością będzie potrzebowało radiatora.

To samo dotyczy rezystora R3. W zależności od wartości płynącego prądu oraz wybranej wartości tego rezystora, jego temperatura może być wysoka.

Podsumowanie

Skonstruowanie sterowanego źródła prądowego nie jest bardzo skomplikowane. Trudno jest popełnić błąd rysując schemat elektryczny lub realnie łącząc taki układ "na stole", ponieważ nie zawiera on wielu elementów. Największą trudnością w przedstawionym układzie jest odpowiedni dobór komponentów, w których należy zwracać uwagę na kilka kluczowych parametrów.

W ramach zadania dla Ciebie :-) możesz obliczyć maksymalną wartość rezystancji obciążenia, którą może obsłużyć przedstawiony układ - dla pełnego zakresu napięć wejściowych! ;-) W razie problemów posiłkuj się obliczeniami wykonanymi tutaj. Powodzenia!