Źródło prądowe można w praktyce zrealizować na wiele sposobów. Czy można jednoznacznie stwierdzić, który z nich jest najlepszy? Zdecydowanie nie. Można jedynie stwierdzić, który jest najlepszy w konkretnym zastosowaniu. Inaczej skonstruowane będzie źródło prądu wykorzystywane w urządzeniach pomiarowych, a inaczej źródło, którego przeznaczeniem jest zasilanie jednej LED dużej mocy. W jednym z nich wymagana może być precyzja, w drugim nie. Z tego powodu, każde rozwiązanie będzie posiadało swoje wady i zalety, których powinieneś być świadomy.
W tym wpisie przedstawię przykłady realizacji tranzystorowych źródeł prądowych wraz z podstawowymi obliczeniami. Dla każdego z opisywanych/projektowanych poniżej układów przyjmuję określone założenia:
- napięcie zasilające: 12 V,
- prąd wyjściowy: 20 mA (tolerancja 10%),
- rezystancja obciążenia: 1 Ohm,
- wszystkie wartości rezystancji należą do szeregu E24.
Jeśli temat źródeł prądowych jest Ci obcy zapoznaj się w pierwszej kolejności z podstawami.
Spis treści
Tranzystorowe źródło prądowe
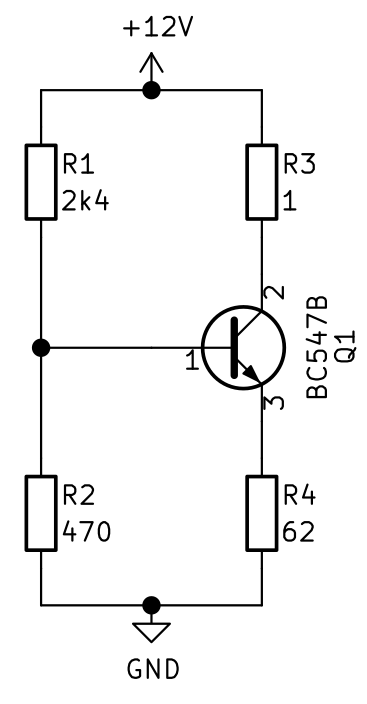
Najprostsze tranzystorowe źródło prądowe można zrealizować wykorzystując jeden tranzystor bipolarny i kilka rezystorów.
Jak działa układ?
Rezystory R1 oraz R2 tworzą dzielnik napięcia, który ustala punkt pracy tranzystora. Zgodnie z prawem Kirchhoff'a spadek napięcia na rezystorze R2 jest równy sumie spadków napięć na złączu BE tranzystora i rezystorze R4.
Rezystory dzielnika napięcia powinny być dobrane tak, aby spadek napięcia na rezystorze R2 był większy od spadku napięcia na złączu BE tranzystora. Wtedy prąd płynący przez R4 można obliczyć:
Prąd ten jest sumą prądów płynących przez bazę i kolektor tranzystora. Zakładając duże wzmocnienie tranzystora, prąd bazy jest pomijalny. Wtedy wyliczony powyżej prąd jest prądem płynącym przez obciążenie źródła - R3.
Przykład obliczeń dla prądu 20 mA
Obliczenia należy zacząć od wyliczenia wartości rezystancji dzielnika napięcia. Znana jest wartość napięcia zasilającego (12 V). Pożądaną wartością napięcia na wyjściu dzielnika (czyli na rezystorze R2) są 2 V. Zakładam wartość 470 Ohm dla rezystora R2 (od czegoś należy zacząć :-) ).
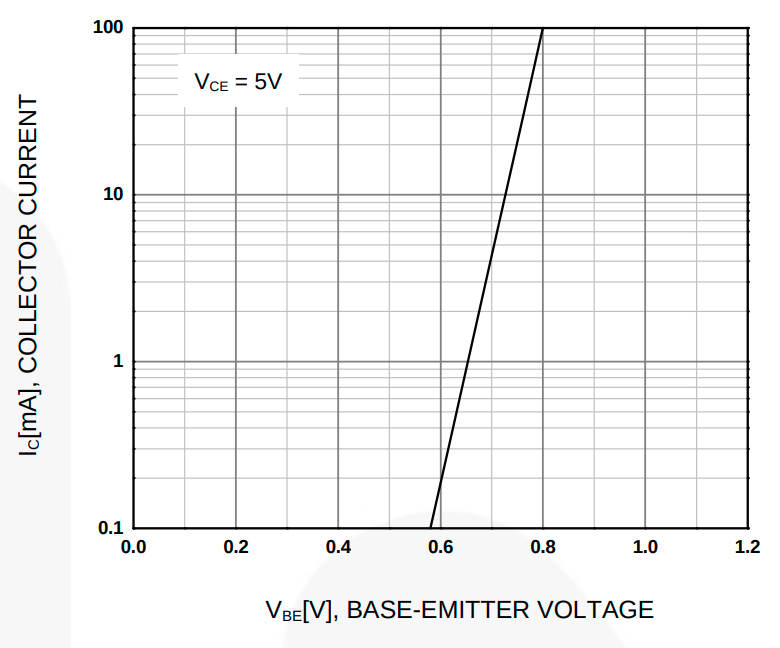
Po obliczeniu wartości rezystancji w dzielniku napięcia, pozostała do obliczenia wartość rezystancji R4. W tym celu należy, na podstawie nowy katalogowej wybranego tranzystora (w tym przypadku BC547), oszacować jaki będzie spadek napięcia na złączu BE, przy prądzie kolektora równym 20 mA. W tym przypadku będzie to około 0.75 V.
Przekształcając wzór (2) można obliczyć R4.
Po wykonaniu obliczeń warto wykonać symulację układu, żeby mieć pewność, że wszystko działa prawidłowo.
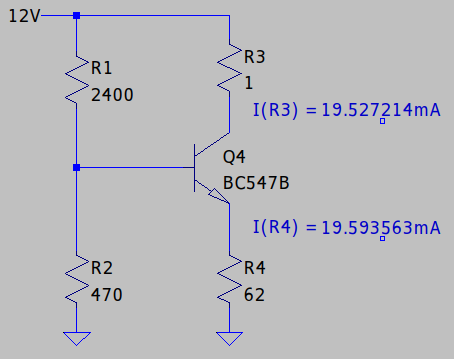
Symulacja potwierdza działanie układu. Wartość prądu płynącego przez obciążenie wynosi 19.5 mA - i taka wartość mieści się w założonym na początku przedziale (tolerancja 10%).
Tranzystorowe źródło prądowe z diodą
Druga propozycja niewiele różni się od pierwszej. Zamiast rezystancyjnego dzielnika napięcia zastosowano tu dwie szeregowo połączone diody. Diody te można również zastąpić diodą Zenera. Użycie w układzie diody jako stabilizatora napięcia sprawia, że źródło będzie pracowało prawidłowo w szerszym zakresie napięć zasilających - będzie odporne na zmiany/wahania napięcia zasilającego (przedstawię Ci to na symulacji poniżej).
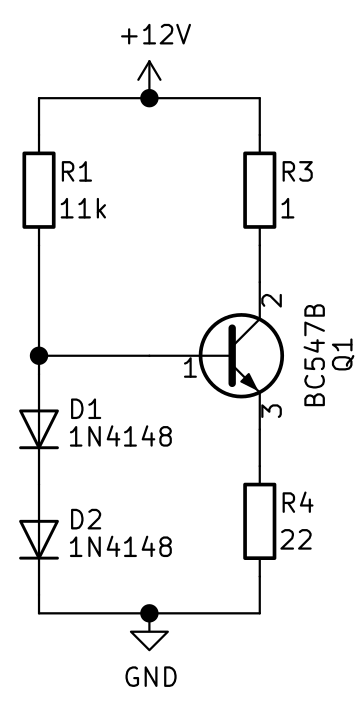
Jak działa układ?
Prąd przepływający przez dwie szeregowo połączone diody powoduje powstanie na nich spadku napięcia, który ustala punkt pracy tranzystora. Zgodnie z prawem Kirchhoff'a suma spadków napięcia na dwóch diodach jest równa sumie spadków napięć na złączu BE tranzystora i rezystorze R4.
Dla danej wartości prądu płynącego przez diody, można odczytać (z noty katalogowej) występujący na nich spadek napięcia. Znając tę wartość można obliczyć prąd płynący przez rezystor R4.
Przyjmując takie same założenie jak w pierwszym układzie - prąd ten będzie równy prądowi płynącemu przez obciążenie źródła.
Przykład obliczeń dla prądu 20 mA
Obliczenia należy zacząć od wyliczenia wartości rezystancji R1, tak, aby prąd płynący przez diody wynosił 1 mA. Znana jest wartość napięcia zasilającego (12 V).
Na początku należy odczytać z noty katalogowej wybranej diody (tutaj 1N4148), jaki spadek napięcia występuje na niej przy prądzie 1 mA. Wartość tę, zgodnie z wykresem można oszacować na 0.6 V.
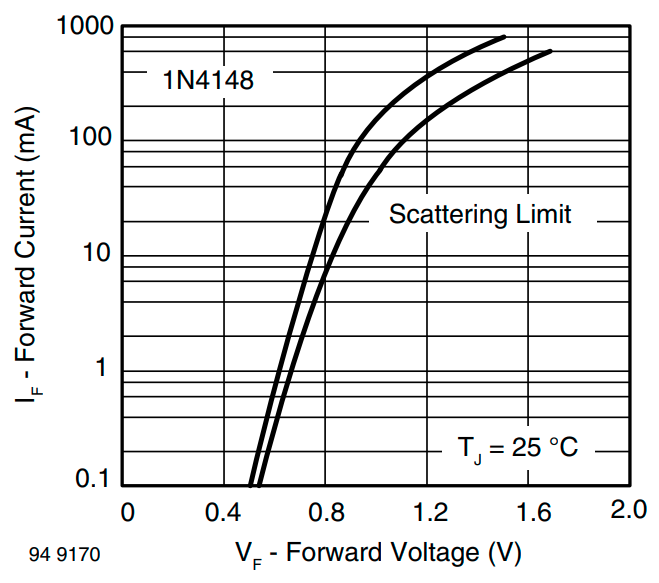
Znając wartość spadków napięć na diodach można obliczyć wartość rezystancji R1.
Reszta obliczeń jest analogiczna do obliczeń w pierwszym przykładzie. Korzystając ze wzoru (8) oraz (9) można wyznaczyć wartość rezystancji R4, która określa wartość prądu obciążenia.
Czas na symulację!
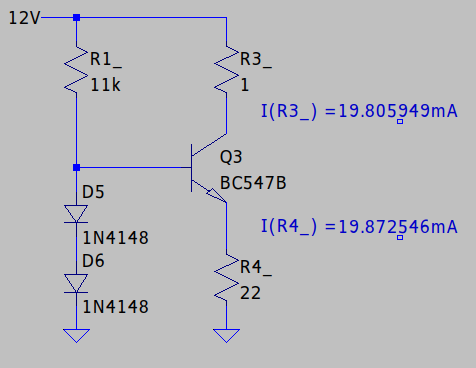
Symulacja ponownie potwierdza działanie układu. Wartość prądu płynącego przez obciążenie wynosi 19.8 mA - i taka wartość również mieści się w założonym na początku przedziale (tolerancja 10%).
Porównanie źródła z diodą i bez diody
Przedstawione powyżej źródła mają swoje wady - prąd wyjściowy jest zależny od wahań napięcia zasilania oraz od temperatury otoczenia. Mimo tego są często spotykane i możesz je bez przeszkód zastosować w prostych układach nie wymagających precyzji.
Skoro dwa przedstawione przykłady są do siebie podobne i nie nadają się do zastosowania w precyzyjnych układach, to po co wspominać obydwa? Źródło z diodą ma jedną, dużą zaletę, której nie posiada jej odpowiednik bez diody - wartość prądu wyjściowego w mniejszym stopniu zależy od napięcia zasilania, lub inaczej mówiąc, będzie pracowało zgodnie z założeniami w szerszym zakresie napięć zasilających.
Na poniższej symulacji przedstawiona jest zależność prądu płynącego przez obciążenie od napięcia zasilania.
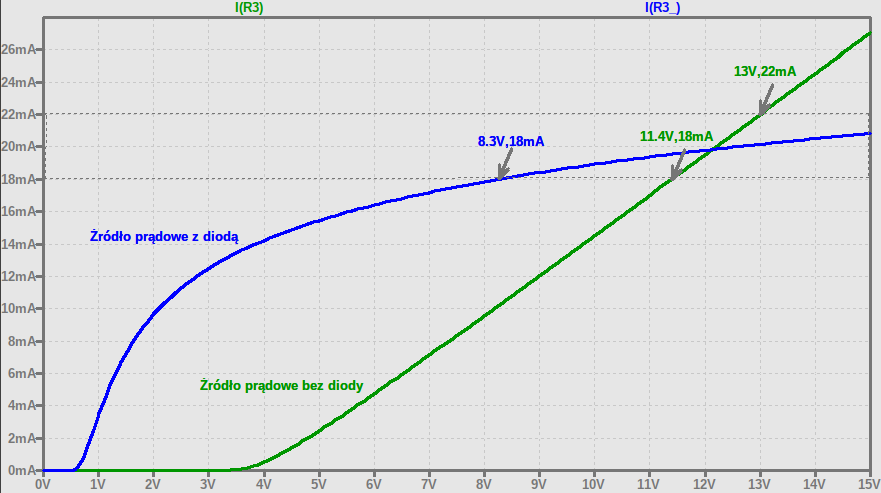
Zgodnie z założoną tolerancją (10%) dla projektowanego źródła prądowego, zakres prądu płynącego przez obciążenie uznajemy za poprawny jeśli znajduje się w zakresie od 18 mA (20 mA - 10%) do 22 mA (20 mA + 10%). Został on na wykresie oznaczony poziomymi, przerywanymi liniami.
W przypadku układu bez diody (zielony wykres), przy spadku napięcia zasilającego o 0.6 V (do 11.4 V) lub zwiększeniu o 1 V (do 13 V) źródło przestaje spełniać założenia projektowe. Źródło z diodą (niebieski wykres) spełnia założenia nawet przy spadku napięcia zasilającego o 3.7 V (do 8.3 V). Różnica wynika stąd, że przy zmniejszaniu napięcia zasilania, napięcie na wyjściu dzielnika rezystancyjnego spada proporcjonalnie do spadku napięcia zasilania. W układzie z diodą, przy zmniejszeniu napięcia zasilania, zmniejsza się prąd płynący przez diody, ale spadki napięć początkowo pozostają na podobnym poziomie - co jest związane z ich nieliniową charakterystyką.
Obliczanie maksymalnej wartości rezystancji obciążenia
W przedstawionych układach, jako obciążenie, podłączony jest rezystor 1 Ohm. Czy można tę wartość zmieniać w dowolny sposób? Zdecydowanie nie. Źródła te mają swoje "maksymalne obciążenia jakie mogą poprawnie obsłużyć" - i jest to związane z maksymalnym napięciem jakie mogą dostarczyć do obciążenia. Jeśli chcesz dowiedzieć się na ten temat więcej sprawdź podstawowe informacje o źródłach prądowych.
Jak więc obliczyć maksymalne obciążenie przedstawionych źródeł? Rozpatrzę przypadek pierwszego z nich (z dzielnikiem napięcia).
Zgodnie z prawem Kirchhoff'a, dla gałęzi z obciążeniem źródła możemy napisać:
Znając prąd płynący w gałęzi możemy obliczyć spadki napięć na rezystorach R3 i R4:
Znając napięcie zasilania oraz powyższe spadki napięć na rezystorach, możemy obliczyć napięcie za złączu CE tranzystora (po przekształceniu wzoru (20)):
Czy te napięcia będą zawsze takie same? Nie. Zwiększając rezystancję obciążenia, zwiększa się na niej spadek napięcia. Jednocześnie będzie zmniejszała się wartość napięcia na złączu CE tranzystora. Do jakiej wartości spadnie napięcie na złączu CE? Najprościej przyjąć, że wartość ta spadnie do wartości napięcia nasycenia złącza CE. Wartość tę można odczytać z dokumentacji - przyjmuję wartość 250 mV (wartość ta zależy od wielu czynników, ale do szacunkowych obliczeń wystarczy).

Mając tę wartość możemy obliczyć maksymalny spadek napięcia jakie będzie mógł wystąpić na rezystancji obciążenia przy prądzie 20 mA (bo na taki prąd projektowane jest źródło):
Znając maksymalny spadek napięcia, jaki może pojawić się na obciążeniu, oraz prąd źródła, z łatwością można obliczyć maksymalną wartość rezystancji obciążenia (prawo Ohma):
Z powyższych obliczeń wynika, że do zaprojektowanego źródła (z dzielnikiem rezystancyjnym) można podłączyć obciążenia w zakresie od 0 Ohm do 525 Ohm. Sprawdźmy co na ten temat powie symulacja! :-)
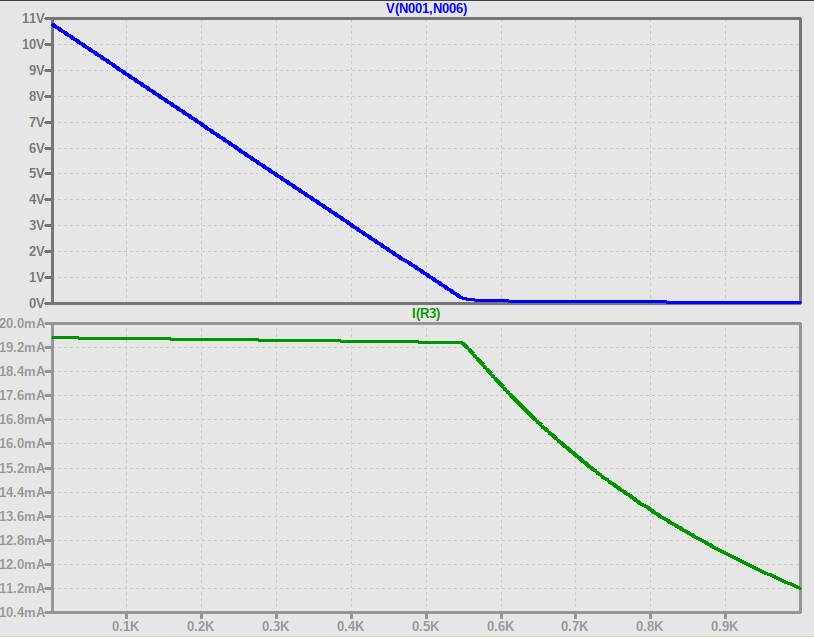
Na powyższych wykresach można zaobserwować, że wraz ze wzrostem rezystancji obciążenia spada napięcie na złączu CE tranzystora (niebieski wykres), i osiąga swoje minimum (około 0.25V) przy rezystancji około 550 Ohm - i to zgadza się z naszym oszacowaniem! Jednocześnie prąd obciążenia pozostaje praktycznie niezmienny do czasu osiągnięcia przez tranzystor napięcia saturacji - później prąd zaczyna gwałtownie spadać wraz z dalszym wzrostem rezystancji obciążenia.
Podsumowanie
Mam nadzieję, że powyższe przykłady tranzystorowych źródeł prądowych, poparte łatwymi obliczeniami i symulacjami pomogą Ci zrozumieć zasadę ich działania. Źródła te do dziś są bardzo popularne i wykorzystuje się w wielu układach elektronicznych oraz układach scalonych.